Геометрический анализ до-династической египетской вазы

Египетская ваза
До-династическая египетская ваза
Происхождение:	Древний Египет
Страна нахождения:	США
Возраст:	> 5000 лет
Музей:	Частная коллекция

В данной статье мы продолжаем рассказывать о последующих выводах, полученных в ходе анализа данных сканирования Египетской гранитной вазы (далее – объект или артефакт), относящейся к додинастическому периоду, возрастом более 5000 лет, опубликованных ранее в предварительном исследовании.

Предисловие

Авторство

Этот материал подготовил Марк Квист. Работа по анализу и моделированию, необходимая для его создания, является результатом совместных моих усилий и другого инженера, который по профессиональным причинам предпочел остаться неизвестным. Все упоминания "мы" в данной статье относятся к авторам. Когда в тексте используется местоимение "я", оно обозначает мое собственное мнение, наблюдение или вывод.

С того момента, как мы получили доступ к данным, мы усердно трудились, чтобы лучше понять этот удивительный артефакт, и добились значительных успехов.

Нам еще предстоит многое узнать, но мы хотели бы поделиться тем, что мы уже знаем на данный момент. Мы совсем не могли предвидеть, что выяснится в ходе этого исследования и насколько необычна эта ваза.

Хотя мы пока не можем делать прямые выводы о том, кто и когда сделал данный артефакт, мы теперь, по крайней мере, знаем гораздо больше о возможностях его создателей.

Это довольно обширная статья. Если вы хотите узнать, стоит ли тратить свое время, вы можете пропустить этот раздел и сначала прочитать выводы, которые, я уверен, привлекут ваше внимание. Однако, если у вас хватит терпения, я бы порекомендовал читать в установленном порядке; здесь есть много интересной информации о нашем исследовании.

Математический метод исследования

Определение радиана в круге

Мы планируем использовать некоторые математические методы для иллюстрации различных моментов исследования. Мы старались сделать их максимально простыми для понимания, предполагая, что читатели обладают базовым пониманием геометрии и алгебры. Некоторые разделы будут включать более сложные уравнения, необходимые для подтверждения точности нашей модели, но они необязательны для общего понимания статьи.

Мы приложим все усилия, чтобы основные моменты были понятны даже тем, кто не интересуется математикой и геометрией. Так что, если эти части для вас ничего не значат, смело пропускайте их.

В этой статье мы будем использовать радианы, поскольку они представляют собой универсальный способ описания углов. Радианы основаны на фундаментальном соотношении между радиусом и длиной окружности, в то время как градусы представляют собой просто произвольное разделение круга на 360 частей. Градусы не основаны на фундаментальных математических соотношениях и не так хороши для такого анализа. Радианы наиболее предпочтительны, поскольку они более ясно отражают основные математические соотношения.

Радианы могут вызвать непонимание, если вы с ними не знакомы, но не бойтесь! На самом деле это проще и более интуитивно понятно, чем использование других единиц измерения. Важно знать, что в круге содержится $2\times \pi$ радиан, а в треугольнике — $\pi$ радиан. Например, угол в $45^{\circ }$ равен ${\frac {\pi }{4}}$ радиан. Любой угол можно описать простыми дробями через $\pi$.

Методология

Первоначальные выводы

Сразу после публикации данных сканирования артефакта, мы провели первоначальный геометрический анализ, результаты которого выявил высокий уровень геометрического соответствия не только между внешними и внутренними элементами, но и в углах и соотношениях размеров.

Эти результаты демонстрируют, что создание данного артефакта было тщательно спланировано, и он не появился случайным образом. Видно, что за ним стоял осознанный замысел, и его форма была продумана с конкретным и последовательным подходом, не сводящимся к хаотичному процессу.

Единицы, меры измерения

В этой статье абсолютные измерения представлены в миллиметрах (мм или "mm") или микрометрах (мкм или "μm"), если не указано иное. Углы указаны в радианах. Все измерения, упомянутые здесь, были получены из данных при лазерном сканирования артефакта.

Измерения были проведены в приложении Blender, а параметрические 3D-модели были созданы с использованием OpenSCAD. Исходный код модели для SCAD можно скачать по ссылке. Мы указали размеры артефакта в миллиметрах и провели измерения, тщательно выравнивая инструменты с вершинами и пересечениями плоскостей.

Все графики и 3D-модели, представленные в этой статье, являются ортографическими проекциями. В 3D модели была применена искусственное освещение и текстура на основе фотографии артефакта, чтобы визуально выделить его изгибы и особенности. Текстура модели предназначена исключительно для иллюстрации и не отражает реального внешнего вида поверхности.

Мотивы данного исследования

Первоначальный анализ и последующий вывод стали стимулом для более глубокого исследования данного артефакта. В этой работе мы стремились создать математически последовательную и полную модель, способную описать все ключевые характеристики физического артефакта.

Мы предположили, что, если такая математическая модель действительно существует, то можно продемонстрировать ее соответствие реальному артефакту. Это поможет в итоге нам лучше понять, какими методами, принципами и знаниями обладали разработчики артефакта,. Анализируя самый простой способ создания дизайна артефакта, мы сможем сформировать представление о минимальных требованиях, необходимых для проектирования.

В настоящее время я обобщаю наши выводы в этой статье, но стоит отметить, что это совместная работа, результат усилий группы людей. Без их вклада мы бы не продвинулись так далеко в нашем понимании.

Гипотеза проектирования

При проектировании артефакта, будь он для функционального или просто эстетического назначения, есть множество подходов. Конечно, дизайнер может просто интуитивно разместить различные его элементы, без каких-либо основных правил, ограничений или принципов, но практически архитектура, искусство и дизайн следуют наборам последовательных принципов при построении.

Существуют различные системы дизайн-принципов, известные с древности, и когда мы наблюдаем красоту, полноту и гармонию формы, это зачастую происходит именно из-за умелого применения таких принципов. Исходя из предварительного анализа артефакта, мы сочли целесообразным исследовать, использовались ли при его создании подобные принципы, и если да, то в какой степени.

Важную информацию, которую можно извлечь с помощью данного подхода, является степень взаимосвязи различных шаблонов для формирования ограничений. В дизайне такие ограничения часто используются для определения различных аспектов индивидуальных элементов, составляющих конечный продукт.

Если мы можем воссоздать артефакт из относительно простого набора дизайнерских приёмов и ограничений, которые задают низкий уровень взаимосвязи или, даже, если такие связи вообще отсутствуют, и все элементы кажутся интуитивно или случайно распределенными, это указывает на артефакт с относительно низким уровнем сложности дизайна или такой, который мог быть создан полностью интуитивным способом.

И наоборот, если мы постоянно видим элементы, определенные сложными взаимосвязями между различными элементами, это указывает на высокий уровень сложности дизайна и то, что требовался более высокий уровень абстракции; не только при создании дизайна, но и при его передаче для производства к конечному появлению.

Параметрическая модель

Чтобы разобраться, как создавался этот артефакт, мы начали с измерения и записи максимально возможного количества его характеристик. Мы также старались выявить повторяющиеся шаблоны в расположении и размерах, а также математически значимые соотношения.

Изначально нам не было ясно, какие именно принципы лежат в основе обнаруженных закономерностей. Тем не менее, было очевидно, что в артефакте существует множество таких регулярных закономерностей и постоянных соотношений. Эти закономерности не только повсеместно есть в модели, но и демонстрировали высокую степень повторяемости, что мы подозревали, будто они выводятся из определенных математических формул.

В результате мы решили провести эксперимент: создать модель в CAD, используя только математические концепции для определения размеров и расположения особенностей артефакта, при этом отказались от любых ручных корректировок модели. Все элементы оказались взаимосвязанными друг с другом.

Мы также установили предельную погрешность модели на уровне 75 микрометров, чтобы оценить, насколько точно, что она соответствует реальным характеристикам артефакта.

Это может показаться абсурдным на первый взгляд создать максимально точную модель древней каменной вазы в CAD и проделать над ней математический анализ, но тем не менее результаты говорят сами за себя. Кроме того, данную модель может скачать любой желающий.

Абстракции высеченные в камне

Для того чтобы создать общее понимание того, что представляет из себя данный артефакт, мы рассмотрим несколько основных принципов проектирования. Далее мы опишем, как эти принципы взаимодействуют между собой, формируя различные формы.

Радиальная траектория

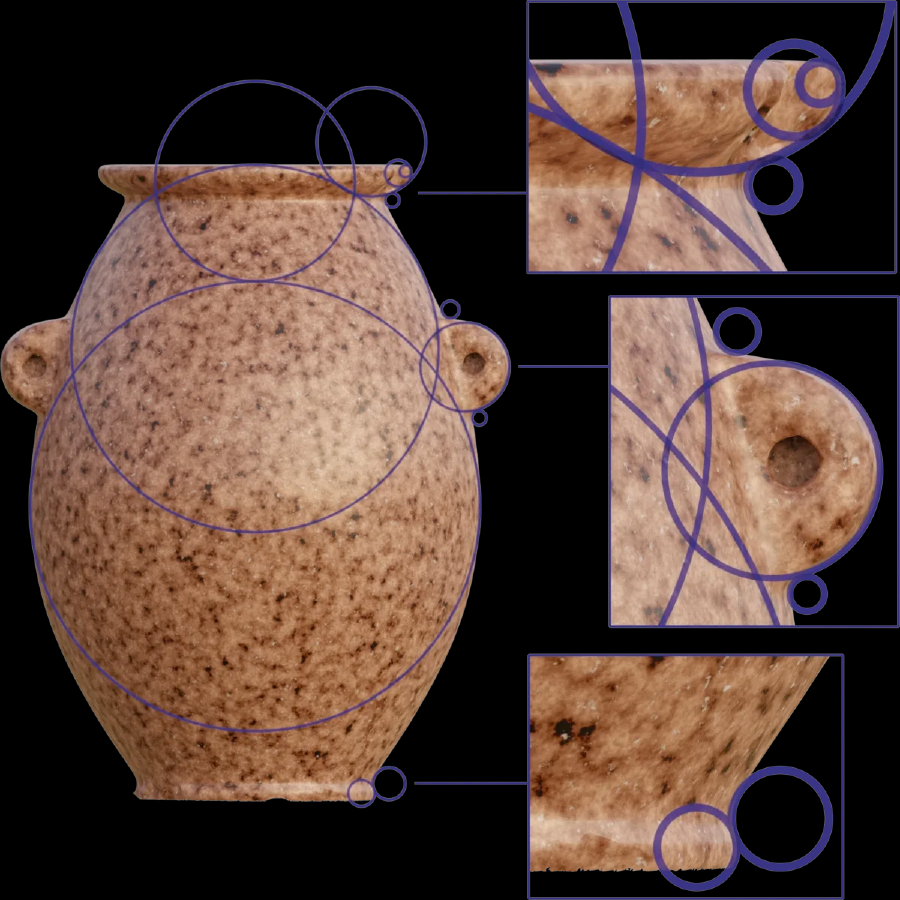
Наиболее часто используемой основной формой в артефакте является круг. Эти круги и его дуги используются для определения большинства особенностей артефакта - все круглые его элементы имеют радиусы, которые взаимосвязаны с невероятной последовательностью и точностью.

На самом деле, существует всего одно уравнение, задающее размеры почти всех кругов, используемых в дизайне. Несколько кругов, не следующих этому шаблону, были специально выбраны для отображения некоторых очень значимых чисел, к которым мы скоро перейдем. Но пока давайте рассмотрим уравнение, определяющее радиусы:

$R(n)=\left({\frac {\sqrt {6}}{2}}\right)^{2}$

С помощью этого уравнения мы можем создавать все необходимые радиусы для формирования артефакта. Мы сможем просто понять, как это уравнение работает, если рассмотрим его с геометрической точки зрения.

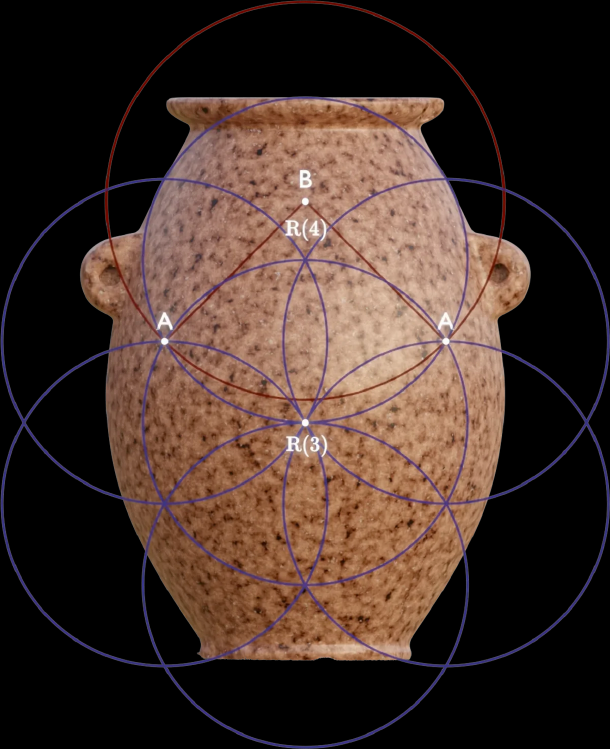
Уже в начальных исследованиях нам стало ясно, что многие особенности кажутся связанными с определенной геометрической конструкцией (шаблоном) единичных окружностей, известной как "Цветок Жизни". Мы также обратили внимание, что использовались не просто одна, а несколько таких шаблонов. Вышеуказанное уравнение представляет собой самое простое описание того, как эти шаблоны взаимосвязаны.

Давайте рассмотрим два этих взаимосвязанных шаблона, состоящих из окружностей $R(3)$ и $R(4)$. Важно отметить, что мы не делали произвольных решений относительно этих шаблонов. Их размеры и расположение относительно друг друга определяются вышеуказанным уравнением (и мы вскоре увидим, как именно). С помощью этих двух шаблонов мы уже можем определить несколько особенностей артефакта:

• 

• A: Верхняя точка артефакта (отклонение: 7 мкм)
• B: Максимальное отступление изогнутой верхней части (отклонение: 13 мкм)
• C: Максимальный диаметр изгиба (отклонение: 72 мкм)
• D: Максимальный диаметр внутренней полости (отклонение: 161 мкм)
• E: Нижняя часть артефакта (точное отклонение неопределенно из-за нерегулярности данных сканирования в нижней части)

Дизайн артефакта поднимается и опускается к разным частям шаблонов "Цветков Жизни", используя элегантную геометрическую конструкцию:

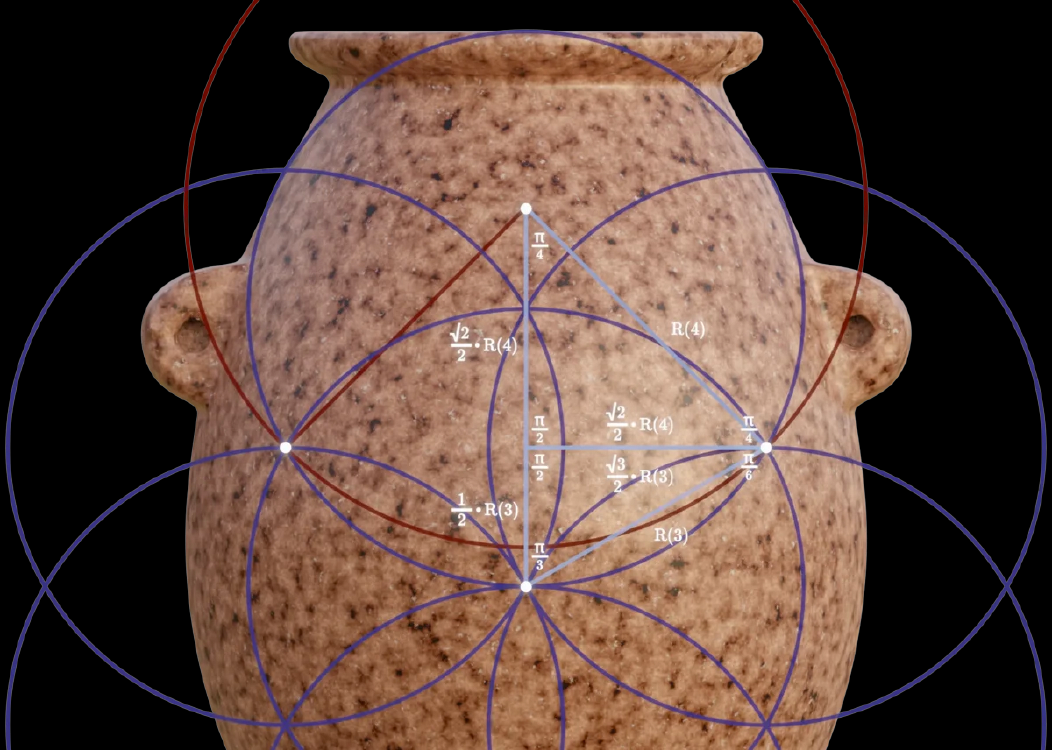
• Давайте выберем две точки пересечения $(A)$ на шаблоне $R(3)$, разделенные на ${\frac {1}{3}}$ от полного круга.
• Теперь мы проведем линию из каждой точки под углом ${\frac {\pi }{4}}$ радиана ($45^{\circ }$).
• В точке пересечения этих линий $(B)$ мы создаем центр нового круга и продлеваем его радиус к одной из первых двух точек.

• 

Теперь отношение радиусов двух окружностей равно ${\frac {\sqrt {6}}{2}}$. Чтобы ясно понять, почему это так, мы можем внести следующие треугольники в конструкцию:

• 

Поскольку у этих двух треугольников одна сторона равна, мы можем использовать это, чтобы показать соотношение:

${\frac {\sqrt {(2)}}{2}}\times R={\frac {\sqrt {(3)}}{2}}\times r\Longrightarrow {\sqrt {(2)}}\times R=$

${\sqrt {(3)}}\times r\Longrightarrow {\frac {R}{r}}={\frac {\sqrt {(3)}}{\sqrt {(2)}}}={\sqrt {({\frac {3}{2}})}}={\frac {\sqrt {6}}{2}}$

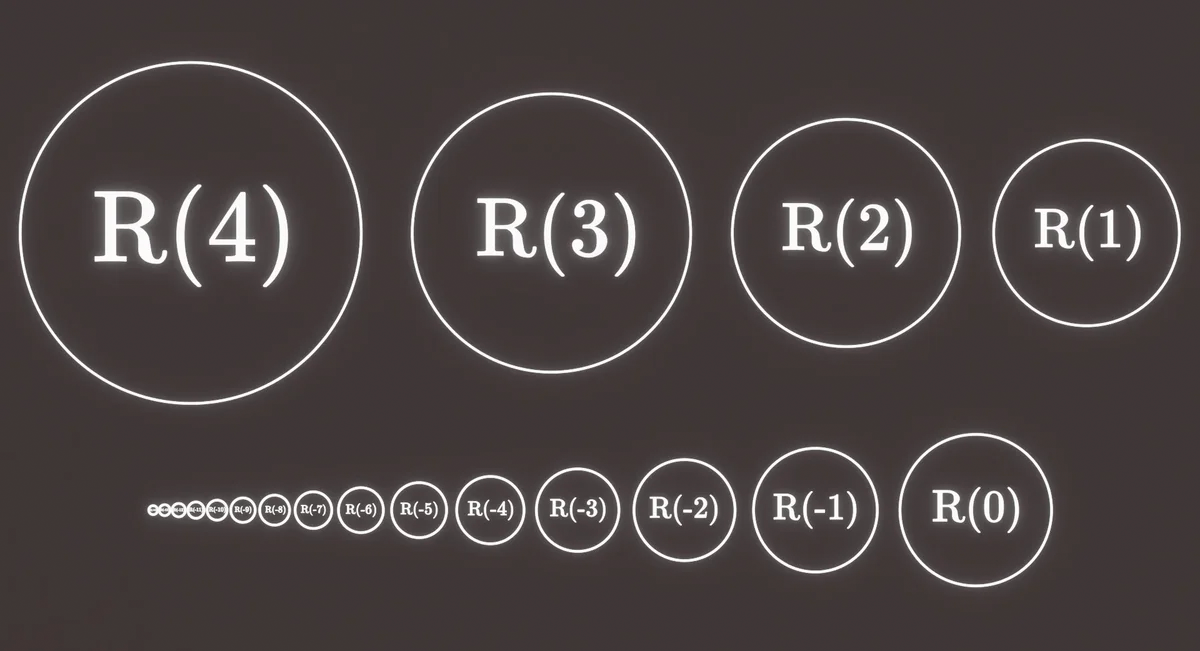
Продолжая этот шаблон, мы получаем функцию $R(n)={\biggl (}{\frac {\sqrt {6}}{2}}{\biggr )}^{n}$, и таким образом можно создать радиусы, используемые в артефакте:

• 

Поскольку этот шаблон широко используется в артефакте, в оставшейся части статьи мы будем называть её функцией радиального обхода $R(n)$.

Благодаря этой конструкции мы можем учесть большинство круглых элементов артефакта. Все круги, созданные с помощью этой функции, с невероятной точностью соответствуют фактическим радиусам разных частей артефакта.

Для каждого из радиусов, обозначенных на графике ниже, мы определили место, где в артефакте сильнее всего отклоняется от математически чистого представления функция $R(n)={\biggl (}{\frac {\sqrt {6}}{2}}{\biggr )}^{n}$, и собрали эти статистические данные по всем наблюдаемым радиусам:

• Минимальное радиальное отклонение составляет 3 микрометра.
• Максимальное радиальное отклонение составляет 68 микрометров.
• Среднее радиальное отклонение составляет 16.25 микрометра.
• Медианное радиальное отклонение составляет 9 микрометров.

Обратите внимание, что большинство радиусов (включая те, которые проявляют локальные отклонения выше среднего) имеют области, которые можно считать, в смысле слова, идеальными. Во многих местах отклонение настолько мало, что мы не можем с уверенностью сказать, является ли отклонение результатом "недостатков" в артефакте или погрешностей в сканировании. Все радиусы на следующем иллюстрации созданы функцией $R(n)$ и, следовательно, тесно взаимосвязаны:

• 

Было бы очень удивительно увидеть такой уровень постоянства точности всего лишь для двух или трех разных радиусов, созданных на основе чисто математической функции. Но увидеть это совершенно последовательно, с микроскопической точностью, в 12 различных радиусах размером от 1,1 мм до 42,2 мм в гранитном артефакте более чем непостижимо.

Дуга в 1-н радиан

Помимо вышеизложенного принципа формирования изогнутых форм по круговым шаблонам, мы выявили еще один интересный принцип дизайна. Расширение дуг на 1 радиан в конфигурации с кругами, созданными функцией радиального обхода, также используется для формирования некоторых особенностей артефакта.

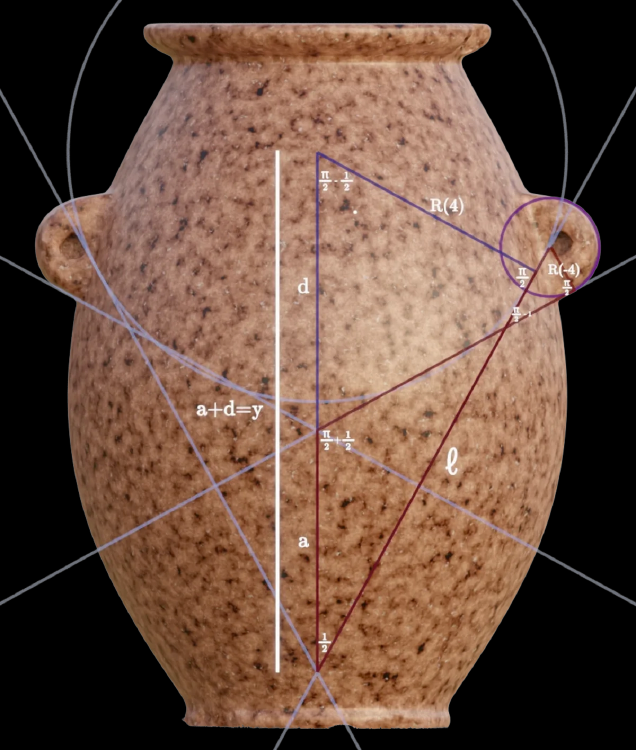
Верхняя часть корпуса над ручками состоит из двух основных областей. Часть непосредственно над ручками имеет небольшую изогнутость, а далее верхняя часть имеет форму идеального конуса. Эту конфигурацию можно определить, расширив дугу на 1 радиан так, чтобы она пересекалась с кругом $R(3)$, который определяет максимальные размеры изгиба верхней части корпуса.

• 

Размещение дуги так, чтобы ее линии касались окружности $R(3)$, идеально отображает коническую область $(A)$. При пересечении с кругом также образуется точка $(B)$, где пересекаются изогнутая и коническая области. Максимальное отклонение конической области от угла в 1 радиан составляет всего 37 микрометров.

Как мы увидим позже, эта дуга в 1 радиан также используется для позиционирования и определения размеров ручек.

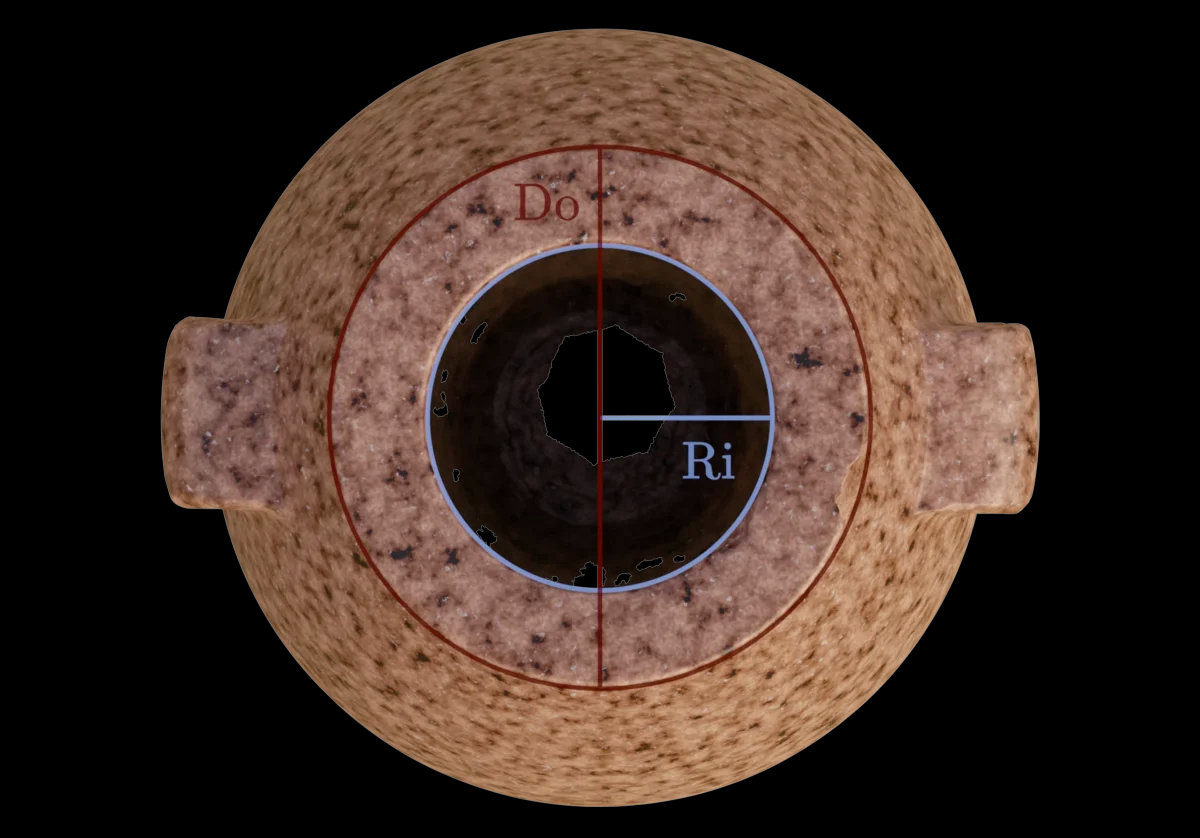
Использование числа π

Функция $R(n)$, которую мы обсуждали ранее, все еще не учитывает некоторые круговые элементы, поэтому давайте рассмотрим, как они были измерены. Отверстие внутри артефакта обладает интересной особенностью: оно слегка сужается внутрь до точки, а затем снова слегка расширяется наружу, прежде чем соединиться с остальной частью внутренней полости.

Даже эта очень тонкая особенность прекрасно описывается кривизной круга $R(6)$. Несмотря на небольшую кривизну, ее достаточно для создания четко определенного минимума внутреннего радиуса отверстия $(Ri)$. Точно так же внешний максимальный диаметр $(Do)$ четко определяется кривизной внешней кромки.

• 

${\frac {Do}{Ri}}={\frac {58.9322}{18.7391}}=3.14488\thickapprox \pi$

$\bigtriangleup ={\biggl (}{\frac {\frac {Do}{Ri}}{\pi }}-1{\biggr )}\times 100=0.1046\%$

Как видно, различие между физическим и идеальным значением π составляет менее 0,11%. Для такого маленького по размерам артефакта такое отклонение составляет около 32 микрометров, что очень маленькое значение. Этот вывод также согласуется с наблюдениями Мариана Марчиша. Кроме того, он обнаружил предварительные доказательства того же соотношения в артефакте, который в настоящее время выставлен в музее Каире.

Вот эксперимент, который вы можете провести дома: попробуйте установить на регулируемом манометре зазор в 32 микрометра. Вы вряд ли сможете наблюдать, как свет проходит через этот зазор. Человеческий волос в два раза толще, чем отклонение коэффициента π в данном объекте. Даже называть это "несовершенством" было бы несколько преувеличенным.

Создатели этого артефакта идеально внедрили число "π" в таком небольшом масштабе в один из самых прочных и труднодоступных материалов. Всё ещё остаются сомнения, что такой результат можно было бы повторить с использованием современного оборудования с числовым программным управлением (ЧПУ).

Использование Золотого Сечения

Так же, как и в случае использования числа π, в дизайн артефакта было включено золотое сечение. Отношение диаметра самой узкой части внешней шейки $(Dn)$ к внутреннему радиусу $(Ri)$ равно золотому сечению $\varphi ^{2}$.

• 

${\frac {Dn}{Ri}}={\frac {49.024}{18.7391}}=2.61613\thickapprox \varphi ^{2}$

$\bigtriangleup ={\biggl (}{\frac {\frac {Dn}{Ri}}{\varphi ^{2}}}-1{\biggr )}\times 100=0.072\%$

Мы снова сталкиваемся с уровнем точности, который мне трудно передать словами, поэтому я предоставлю расчетам говорить сами за себя. В физическом артефакте это крайне маленькое отклонение от математической точности составляет приблизительно 20 микрометров. Как и в случае с использованием числа π, этот результат также соответствует наблюдениям Мариана Марчиша.

Подарок из прошлого

Здесь также обнаруживается золотое сечение, закодированное в соотношении между внешним диаметром горлышка $(Do)$ и радиусом основания $(Rf)$:

• 

${\frac {Do}{Rf}}={\frac {58.9322}{22.5299}}=2.615733\thickapprox \varphi ^{2}$

$\bigtriangleup ={\biggl (}1-{\frac {\frac {Do}{Rf}}{\varphi ^{2}}}{\biggr )}\times 100=0.088\%$

Отклонение в абсолютных измерениях здесь составляет приблизительно 35 мкм. В своего рода математическом подходе создатели артефакта применили здесь двойное соответствие: поскольку $Do$ уже производится с использованием π, радиус основания может быть лучше описан как $Rf={\frac {Ri\times \pi }{\varphi ^{2}}}$. Поскольку это создает эквивалентность между всеми четырьмя измерениями, установленными на основе фундаментальных математических концепций, следующее должно быть логичным продолжением:

$Do=Ri\times \pi \land Dn=Ri\times \varphi ^{2}\land Rf={\frac {Ri\times \pi }{\varphi ^{2}}}$

$Ri=1\Longrightarrow Do=\pi \land Dn=\varphi ^{2}\land Rf={\frac {\pi }{\varphi ^{2}}}$

∴

$1=Ri$

Действительно, я не могу представить более изысканного и красивого способа установления и передачи базовой единицы измерения. Тот, кто создал этот удивительный артефакт, хотел, чтобы мы знали, как выглядит их система измерений, и вот она – заложена в камне, в универсальном языке математики, и дошла до нас через тысячелетия. Просто невероятно!

Поскольку у нас в настоящее время нет более подходящего обозначения, мы будем обозначать используемую в дизайне единицу измерения как U(единицы). Согласно нашим измерениям, приближенное значение этой единицы измерения может быть:

$1U\approx 18.739mm$

Так как мы наблюдали отклонения в размерах в пределах от 20 мкм до 32 мкм при измерениях, используемых для получения этого числа, мы не советуем использовать вышеуказанное приближенное значение в качестве основы для сравнения вне данной статьи.

Тем не менее, мы видим интересную корреляцию в этом числе. Приближенное значение, к которому мы пришли, отличается всего на 2,07 мкм (менее точности сканирования) от точного соответствия длине волны электромагнитной волны с частотой 16 ГГц, распространяющейся в вакууме:

${\frac {c}{f}}={\frac {299,792,458m/s}{16,000,000,000Hz}}=18.737028625mm$

Мы считаем, что это устанавливает более ясную общую точку отсчета, поскольку $1U$ можно определить как простое деление скорости света в вакууме.

Для того чтобы у нас была общая отправная точка и мы могли обсуждать эту единицу, избегая недопонимания, мы предлагаем предварительное определение, основанное на указанном выше соотношении:

$1U=18.737028625mm$

Первоначальные размеры и меры длины

С учетом вышеуказанной данных мы теперь можем увидеть, какими на самом деле были размеры этого артефакта в глазах его создателей. Миллиметры здесь затрудняют передачу какого-либо смысла, но когда мы рассматриваем размеры в единицах $U$, перед нами открывается совершенно другая интересная картина:

Измерения	$U$	мм
Радиус отверстия	$1$	18.74
Высота	${\frac {32}{45}}$	119.9
Ширина	${\frac {9}{2}}$	84.3
Ширина с ручками	${\frac {46}{9}}$	95.7
Максимальный диаметр горлышка	$\pi$	58.9
Минимальный диаметр шейки	$\varphi ^{2}$	49
Радиус основания	${\frac {\pi }{\varphi ^{2}}}$	22.5

Установка ручек артефакта

В этом разделе мы покажем, как были спроектированы ручки. Мы будем использовать немного более сложные математические концепции, что может быть не интересно для всех. Однако мы считаем важным четко объяснить этот процесс, поскольку он является ярким примером того, насколько сложен и взаимосвязан дизайн артефакта. Мы используем математику в качестве конкретного подтверждения этого.

Если вас не интересуют уравнения, вы можете пропустить этот раздел и перейти к следующему, где мы описываем все это более простыми словами.

Геометрия ручек была спроектирована при взаимодействии двух изогнутых линий, которые мы ранее ввели. Первая из этих линий распространяется от центральной точки пересечения $R(3)$ шаблона "Цветок Жизни":

• 

Вторая создается путем построения дуги диаметром 1 радиан касательной по верхнему кругу в сетке $R(4)$ по шаблону "Цветка жизни":

• 

Определив эти две дуги (берущие начало из $R(3)$ и $R(4)$ нашего полученного шаблона "Цветка Жизни) и окружность $R(-4)$, мы теперь имеем ограничения, необходимые для построения геометрии ручек, которые можно выразить в виде полярного вектора $V_{h}$:

• 

$V_{h}=\left[{\frac {\ell }{\theta }}\right]$, где:

$\theta ={\frac {1}{2}}\land \ell ={\frac {{\frac {R(4)}{sin({\frac {1}{2}})}}-{\biggl (}{\frac {1}{2}}\times R(3)+{\frac {\sqrt {3}}{2}}\times R(3){\biggl )}}{sin{\frac {\pi }{2}}-1}}\times$ $sin({\frac {\pi }{2}}+{\frac {1}{2}})+{\frac {R(-4)}{sin{\frac {\pi }{2}}-1}}$, так как

$d={\frac {1}{2}}\times R(3)+{\frac {\sqrt {(3)}}{2}}\times R(3)\land y=$${\frac {R(4)}{sin{\frac {1}{2}}}}\Longrightarrow a=y-d\Longrightarrow$

$a={\frac {R(4)}{sin({\frac {1}{2}})}}-{\biggl (}{\frac {1}{2}}\times R(3)+{\frac {\sqrt {(3)}}{2}}\times R(3){\biggr )}$

$\ell _{1}={\frac {a}{sin({\frac {\pi }{2}}-1)}}\times sin{\biggl (}{\frac {\pi }{2}}+{\frac {1}{2}}{\biggr )}\land \ell _{2}=$${\frac {R(-4)}{sin({\frac {\pi }{2}}-1)}}\Longrightarrow \ell =\ell _{1}+\ell _{2}$

Остальные детали ручек можно объяснить так:

• Прямой угол нижней секции ручки определяется первой дугой в 1 радиан, следовательно, это ${\frac {1}{2}}$ радиана.
• Изгиб, соединяющий прямую часть нижней секции ручки с корпусом, формируется дугой от окружности $R(-13)$. Угол в ${\frac {1}{2}}$ радиана касается этой окружности.
• На сколько мы понимаем, прямая часть верхней секции ручки была намеренно сделана под углом ${\frac {\varphi }{10}}$ радиана.
• Изгиб, соединяющий прямую часть верхней секции ручки с корпусом, определяется дугой от окружности $R(-12)$. Угол ${\frac {\varphi }{10}}$ радиана касается этой дуги.
• Острый наблюдатель заметит небольшую внешнюю особенность на верхнем изгибе ручки (примерно 0,3 мм). Эта особенность точно учтена добавлением немного смещенной окружности $R(-5)$ в геометрию.

Мы не смогли упростить эту конструкцию лучше, чем описано выше, и считаем, что, вероятно, это оптимальная конфигурация для создания ручек с точки зрения простоты. Из этого вытекают существенные последствия.

Физическая геометрия, которую мы наблюдаем в готовом артефакте, по существу создавалось как решение взаимосвязанного набора уравнений, охватывающих весь артефакт в нескольких измерениях и конфигурационных пространствах.

Мы считаем весьма вероятным, что весь артефакт действительно может быть представлен как единое уравнение.

Заключение

Мы уверены, что наша текущая модель наглядно демонстрирует наличие высокого уровня сложных принципов дизайна и сложных взаимосвязей заложенных в данном артефакте.

Хотя мы не можем утверждать с уверенностью, что описание дизайна в этой статье точно соответствует оригинальной задумке создателей, однако мы уверены, что наша модель отражает реальную математику, взаимосвязи и ограничения, присутствующие в дизайне.

Несмотря на то, что остается еще многое, что предстоит узнать об этом удивительном артефакте, знания и данные, которыми мы уже располагаем, позволяют нам с уверенностью сделать некоторые выводы.

Случайности при изготовлении

Мог ли такой предмет возникнуть случайно в процессе его изготовления? Разве могло быть просто совпадение случайных обстоятельств?

Нет. Это предположение было бы слишком наивным и суеверным.

Представьте себе, что абсолютная точность и согласованность между всеми взаимосвязанными частями в этом артефакте возникли просто так. Это просто невозможно. Было бы гораздо более вероятно проснуться однажды утром и обнаружить, что из квантовых флуктуаций в вашей квартире возникла совершенно новая вселенная.

Может быть, в каких-то ситуациях при производстве предметов можно получить соотношения со значениями $\pi$ или $\varphi$, но нужно понимать, что все части в этом артефакте тесно связаны! Изменение одного параметра повлечет за собой изменения во всем остальном. Здесь есть как минимум 15 уровней взаимосвязей, и все они связаны между собой на микроскопическом уровне.

Этот предмет был тщательно и внимательно спроектирован человеком с невероятным уровнем мастерства, понимания и художественного вкуса. В этом нет никаких сомнений.

Требования для проектирования

Какая система была бы необходима для проведения от абстрактного дизайна артефакта до его производства? Возможно ли было бы разработать его аналоговыми методами, например, на бумаге в виде чертежа, который затем использовался бы для последующего изготовления?

Для того чтобы дать удовлетворительный ответ на этот вопрос, нам придется внимательно рассмотреть множество факторов. В будущих статьях мы глубоко рассмотрим этот вопрос, который заслуживает особенного внимания. На данный момент считаем, что наши начальные выводы по этому вопросу стоит здесь кратко затронуть.

При рассмотрении масштабов, на которых была осуществлена точность в этом артефакте, возникают интересные проблемы. Самые маленькие радиусы - которые мы уже выявили в артефакте - составляют всего лишь около 1 мм, но они масштабируются с идеальной точностью через радиальную функцию с микрометровой точностью, даже для самых больших радиусов в артефакте (около 63 мм).

Проведение такого масштабирования на любой аналоговой среде сразу внесло бы ошибки, которые только бы увеличивались с каждым последующим радиальным перемещением. Даже наши современные инструменты черчения, работающие на самой гладкой бумаге, создали бы ошибки, погрешности, близкие к полным радиусам некоторых из этих окружностей и других особенностей.

Чтобы учесть и контролировать такие ошибки, дизайнеру пришлось бы масштабировать чертеж до размеров по меньшей мере нескольких метров, что, конечно же, вызывает еще вопросы о том, как вернуть его обратно к относительно небольшим размерам реального артефакта.

Возможно, наиболее правдоподобным способом представления этого артефакта на аналоговом носителе было бы описать его геометрически и математически. Это вполне возможно, и по пути можно даже делать эскизы, чтобы показать приблизительный дизайн. Нашей известна подобная математика необходимая для такой задачи примерно с 500 года н. э.

Но столкнувшись с масштабированием, затем передачи этого дизайна в производственный процесс для изготовления физического объекта, мы возвращаемся к исходной точке, так как теперь нам нужно создать какой-то аналоговый шаблон, который может направлять или контролировать процесс производства.

Хотя этот аргумент, который я сейчас выдвину, безусловно, требует полного обоснования, я чувствую, что это было бы трусостью с моей стороны не довести этот аргумент до его логического завершения и не настаивать на доказательствах и логике.

На сколько нам известно, никто и никак и никогда прежде, не использовали математические формулы и уравнения в качестве входных данных и не производили действия для управления токарным станком для получения какого-либо результатата.

Среди всех знаний, которые мы накопили со временем, есть одна вещь, которая может решать сложные подобные задачи — это машина Тьюринга. Это устройство может получать данные, сохранять информацию, выполнять определенные действия согласно заранее заданным правилам и выдавать нам определённый результат.

Такие машины могут быт разных форм и размеров, и могут быть созданы как механически, так на электронных принципах или даже пневматическим или гидравлическим способом. И вы сейчас используете одну из таких машин, чтобы прочитать эту статью.

Мы называем этот класс устройств компьютером, и не существует разумного способа представления, управления или производства дизайна этого артефакта, не имея доступа к такому устройству.

Требования для производства

При сравнении результатов нашей модели с физическим артефактом мы получили общее представления о возможностях его создателей. Основываясь только на фактах, мы можем сделать следующие выводы:

• Поскольку у нас нет никаких свидетельств о том, как мог бы происходить процесс обработки гранита, мы предполагаем , что была применена технология резки, резьбы, шлифовки и так далее).
• Создатели артефакта смогли последовательно выдерживать допуски около 30 мкм в процессов обработки гранита. Во многих местах мы видим допуски менее 10 мкм.
• Инструменты, используемые для удаления материала из гранитной заготовки, должны были обладать невероятно высокой стабильностью вдоль оси для достижения подобных допусков.
  • Технологически это возможно только с использованием ультра-гладких и точных стержней, подшипников, винтов и подобных механизмов.

• Должны были быть использованы невероятно точные управляющие механизмы для контроля в процессе обработки, поскольку готовый артефакт соответствует заданному дизайну с ыфсокой точностью.
  • Это требует механической технологии ультра высокого качества, конкурирующей или превосходящей те, что мы можем использовать сегодня.

• Мы не обнаружили заметной потери симметрии или позиционирования при перемещении по кривым различных радиусов или их расположению, что, скорее всего, означает, что создатели артефакта смогли обработать его в один подход или как-то осуществлять смену инструмента с минимальной потерей калибровки положения.
• Установление внешних особенностей артефакта и поддержание точности, особенно в областях между ручками означает, что простой вращательный процесс был бы недостаточен для создания геометрии, которую мы наблюдаем. Другими словами подобное расположение ручек делает невозможным вращательный процесс обработки объекта по любой из осей.
  • Самый простой производственный процесс, который нам удалось предположить для такого объекта, потребовал бы 5 степеней свободы в направляющих инструмента.

Выводы

Исходя из нашего понимания артефакта и знаний об основных ограничениях физики и законах природы, мы приходим к следующим выводам:

• Этот артефакт был создан при помощи сложной системы производства, которое позволяло создать его из одного куска гранита.
• Требования к производству включают в себя, как минимум, сложную механическую технологию и высокоточные компоненты и очень твёрдые материалы для обработки и резки камня.
• Производственная система, вероятно, управлялась автоматизированной системой управления, способной интерпретировать дизайн как входные математические данные и создавать необходимые точные движения механизмов, чтобы добиться подобного результата.
• Для создания и обработки дизайна, а также его передачи в производственную систему, вероятно, использовалась сложная машина, способная делать соотвествующие вычисления.

Мы не можем с уверенностью сказать, кто именно создал этот артефакт, но для такого технологически сложного произведения необходимы высокие навыки и возможности. Эти выводы предоставляют интересные перспективы для будущих исследований происхождения этого артефакта.

Последующее исследование

Мы надеемся, что подобные артефакты (их тысячи находящиеся в музеях по всему миру) будут отсканированы с использованием подобной современной технологии или технологий более высокого уровня. Это позволит провести анализ этих удивительных артефактов и создать обширное исследование.

Благодаря доступным сегодня аналитическим инструментам и технологиям, мы стоим на пороге новой эры исследования нашего прошлого и общего наследия. Невероятно ценным является более глубокое понимание нашего общего происхождения как человечества и как индивидуумов.

Лишь через открытое, критическое и честное научное исследование, основанное на принципах проверенных и конкретных данных, мы можем раскрыть самые глубокие и темные аспекты нашего прошлого.

Нам следует дать фактам говорить самим за себя, без предварительной интерпретации, даже если выводы временно противоречат текущему догматическому пониманию глубокой истории.

В сфере научной деятельности все теории являются предварительными и должны уступать место более простым, лучше соответствующим фактам. Если этот фундаментальный принцип утратит свою значимость, то наука потеряет свою суть, превращаясь из инструмента исследования в догму.

Используемые источники

• Оригинальная статья Abstractions Set In Granite
• Исходная страница с данными исследования: Vase Scan Resources

Исходные файлы исследования

• Характеристики артефакта
• Отсканированная 3D модель артефакта: файл 1, файл 2